理工酷

回顾一下，LDA是一种概率模型，它假设了一组全局主题（即一组单词的离散分布）和一组文档主题（即一组主题的离散分布，每个文档一个分布）。 要生成文档，请从本地主题中反复抽取第n个单词的主题分配，然后通过查找相应的全局主题来绘制该单词。

由于数学上的细节，这些离散分布有一个重要的性质，称为稀疏性。 详细信息是LDA在其离散分布上使用Dirichlet分布作为先验，并且，

1. Dirichlet的充分统计量为[logp1，…，logpK];
2. p1+⋯+pK的和必须为1，因为它是离散概率分布;
3. log为凹函数

这三个事实意味着Dirichlet在使用对称超参数时会惩罚组件（例如主题，单词）的“打开”。直观地想象一下，如果你把一些质量概率加到k上，打开它会发生什么(见下图)。因为p要标准化，这需要把概率质量从所有其他的j≠k的分量中去掉。

p的和仍然为1，但是∑ilogpi下降了，因为log是一个凹函数。在所有其他条件相同的情况下，这会使模型的联合对数似然性下降，这意味着该模型会对非稀疏p进行惩罚。

（有趣的是，这一推理行不需要hyperparameters小于1，通常将其称为稀疏Dirichlet）。

稀疏性很酷，因为它鼓励模型的大多数潜在变量为零（或接近零），并且这很有用，因为它编码了一种信念，即对于数据只有很少（即不是一百个）隐藏的解释 您正在建模。 这些说明可能会有所不同，具体取决于您正在查看的文档，因为LDA是分层模型。

但是，LDA不仅是分层的稀疏模型，而且还非常有趣地是双重稀疏模型。 它权衡了文档主题和全局主题之间的稀疏性。 为什么要权衡？ 因为文档主题分布“偏爱”每个文档更少的主题，而全局主题分布“偏爱”每个主题更少的单词，所以这些目标是矛盾的。

稀疏目标彼此矛盾，因为如果文档主题的稀疏属性发生了变化，则每个文档将只有一个主题，而不是多个主题。 但这意味着，要解释文档中的所有单词，主题在单词上的分布将必须反映整个文档的主题（即，在文档的单词的经验分布下，其超参数为1）， 对于全球主题而言，这并不是一个稀疏的结果。 同样，如果全局主题的稀疏属性得以实现，则每个主题将只有一个单词，这意味着每个文档都必须展示大量主题以解释文档中的单词。

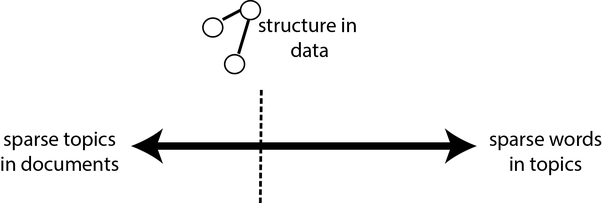
LDA在这两个极端之间找到了平衡，之所以如此有用，是因为这种平衡是由数据中的结构决定的。 此外，之所以比也使用竞争稀疏性的其他模型（例如pLSI）有所进步，是因为余额是在文档级别解决的，而pLSI必须解决整个语料库的余额。

总而言之，LDA之所以有效，是因为它表达了文档主题分布和主题词分布之间的竞争稀疏性。