0
他们处理两种不同的问题。
奈奎斯特定理处理给定带宽信道上的最大信令速率。香农定理涉及从有限数量的样本中重建信号。由于结果相似,因此人们经常将奈奎斯特的名字与采样定理联系起来。但这是不正确的。
在这里,我将解释奈奎斯特定理。
例如,在电报中考虑用于开关键控(ASK)的矩形脉冲: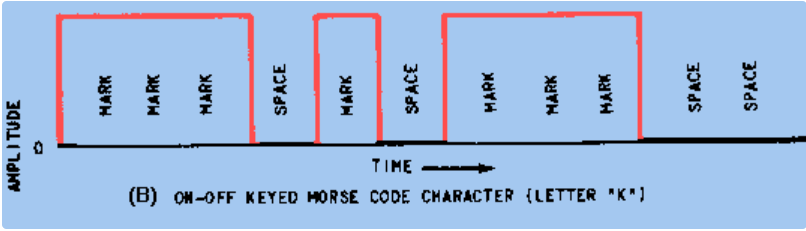 脉冲的频谱特征应与通道的频谱特征相匹配。如果脉冲频谱比通道的频谱宽,则它将被衰减。时域和频域之间的逆关系意味着脉冲将在时域内扩展,从而导致相邻符号周期中的脉冲重叠-这种现象称为符号间干扰。这使得检测困难。
脉冲的频谱特征应与通道的频谱特征相匹配。如果脉冲频谱比通道的频谱宽,则它将被衰减。时域和频域之间的逆关系意味着脉冲将在时域内扩展,从而导致相邻符号周期中的脉冲重叠-这种现象称为符号间干扰。这使得检测困难。
下面显示的是使用矩形脉冲表示符号所产生的ISI。矩形脉冲的频谱是正弦,其频谱扩展到无穷大。因此,任何带宽受限的通道都会对其进行衰减,从而导致信号在时域内扩展。
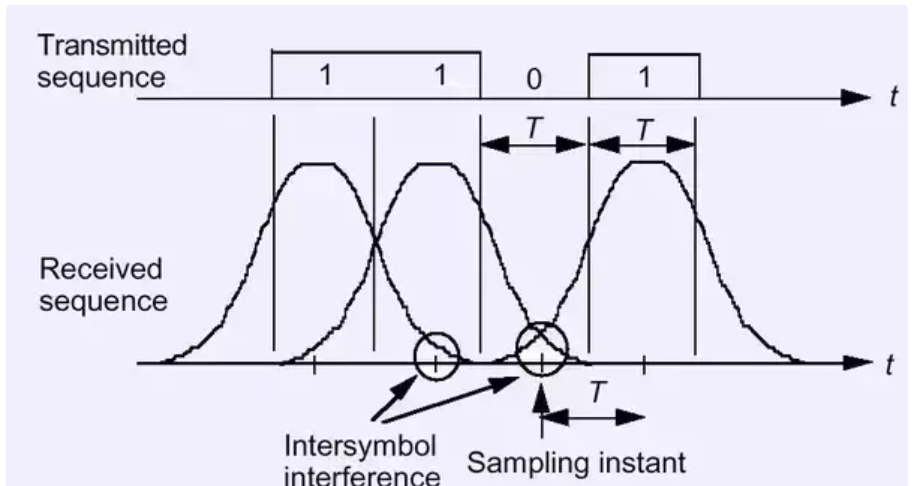
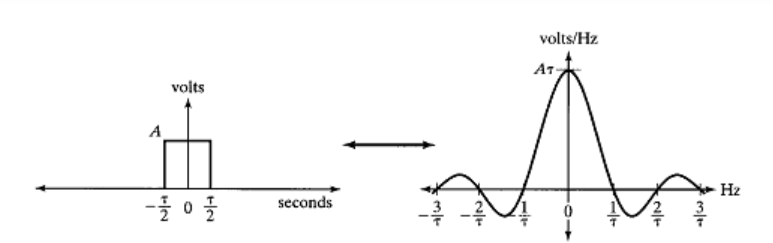 Nyquist建议使用带限脉冲进行传输,而不是限时脉冲。这会将符号间干扰问题转移到时域(从而使滤波器设计变得容易)。
Nyquist建议使用带限脉冲进行传输,而不是限时脉冲。这会将符号间干扰问题转移到时域(从而使滤波器设计变得容易)。
 但是,你将如何处理时域中的ISI?
但是,你将如何处理时域中的ISI?
奈奎斯特观察到,正弦脉冲的零交叉点以t = 1 / 2B秒的间隔出现。因此,如果正弦脉冲以每秒2B脉冲的速率传输,则每个正弦脉冲的峰值将出现在前一个正弦脉冲的第一个零交叉处,因此易于检测。
这是奈奎斯特定理,在一秒钟内可通过带宽B的通道发送的最大带限脉冲数为2B 。该速率是最大可能的速率,因为我们使用的脉冲的带宽恰好等于通道带宽。如果使用带宽较小的脉冲,则时域sinc会变宽,从而扩大零点的位置,从而可能降低信号速率。
收藏
 理工酷
理工酷
 资源下载
资源下载