理工酷

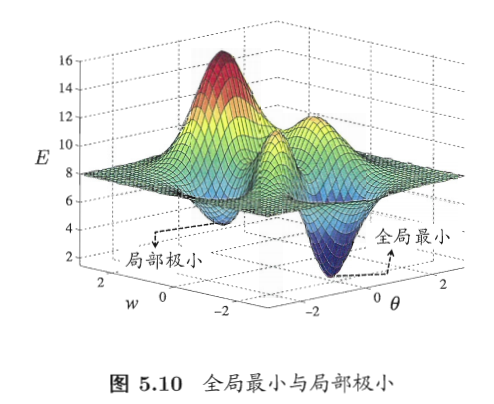
首先我们要理解什么是全局最小和局部最小 局部极小解是参数空间内的某个点，其邻域点的误差函数值均不小于该点的函数值；全局最小解则是指参数空间中所有点的误差函数值均不小于该点的误差函数值。 显然参数空间内梯度为零的点，只要其误差函数值小于邻点的误差函数值，就是局部极小点；可能存在多个局部极小值，但是却只有一个全局最小值。也就是说，全局最小一定是局部最小，反之却不一定成立。 基于梯度的搜索时使用最为广泛的参数寻优方法，在此类方法中，我们从某些初始解出发，迭代寻找最优参数值。每次迭代中，我们先计算误差函数在当前点的梯度，然后根据梯度确定搜索方向。例如，由于负梯度方向时函数值下降最快的方向，因此梯度下降法就是沿着负梯度方向搜索最优解。 若误差函数在当前点的梯度为零，则已达到局部极小，更新量将为零，这意味着参数的迭代更新将再次停止。显然，如果误差函数仅有一个局部极小，那么此时要找到的局部极小就是全局极小；然而，如果误差函数具有多个局部极小，则不能保证找到的解是全局最小。